PaperReading:Efficientnet: Rethinking model scaling for convolutional neural networks
这一篇文章是我阅读论文《Efficientnet: Rethinking model scaling for convolutional neural》的记录。
abstract
摘要部分说明了该论文的内容,本论文提出一种模型缩放的方式并应用于MobileNet和ResNet上以证明有效性, 更进一步,本文设计出了Efficient Nets, 相比于传统的CNN具有更好的效率和准确率。
源码于:
tpu/models/official/efficientnet at master · tensorflow/tpu (github.com)
introduction
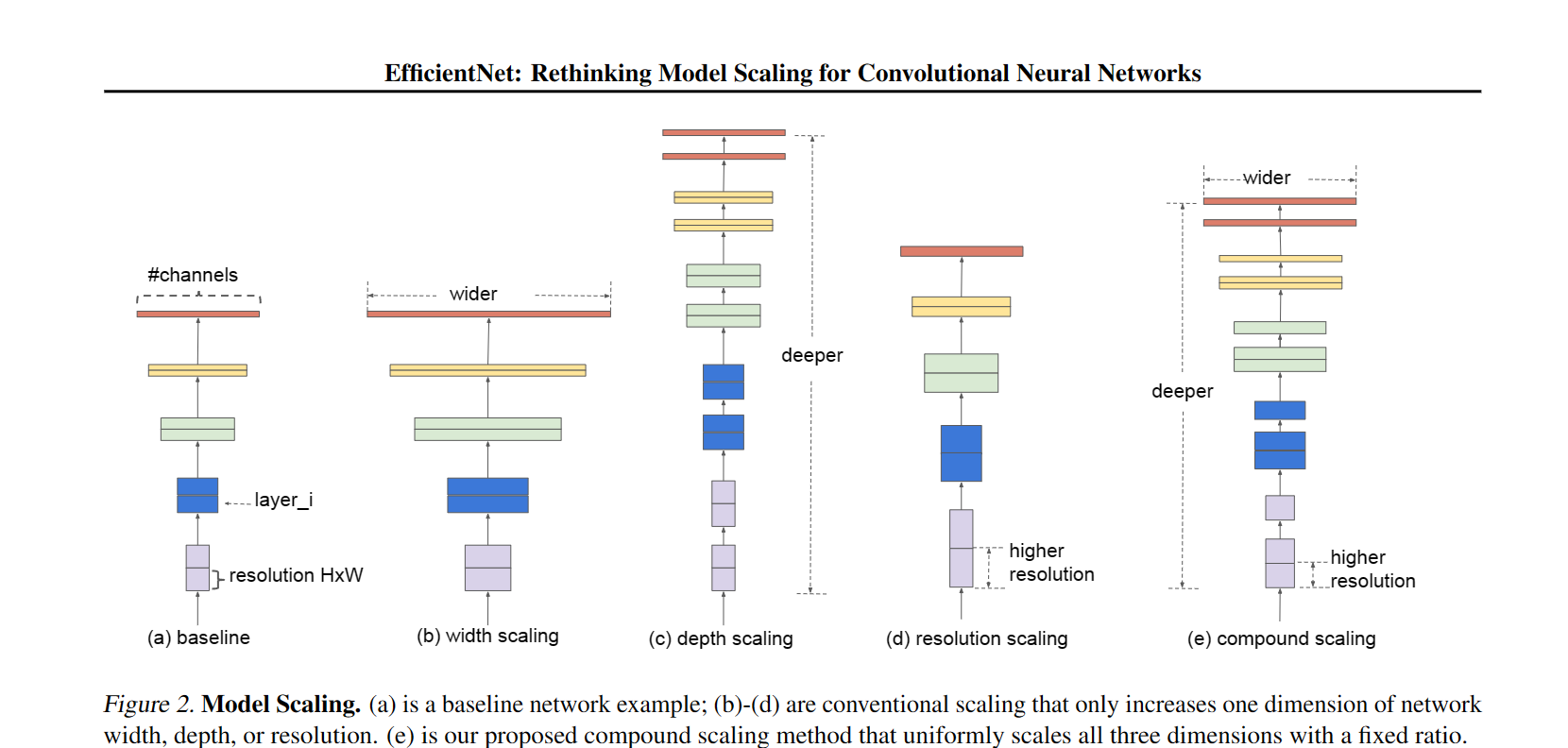
introduction部分的主题思想大概是他们初步的经验化的找到了量化网络的深度宽度和分辨率的方法,即当计算资源扩大\(2^N\)倍时,网络的深度,宽度,以及分辨率分别扩大$N,N,^N \(倍数 ,而\),,$分别由原始网络上的a small grid search决定。
For example, if we want to use 2N times more computational resources, then we can simply increase the network depth by αN , width by βN , and image size by γN , where α, β, γ are constant coefficients determined by a small grid search on the original small model. Figure 2 illustrates the difference between our scaling method and conventional methods
而模型拓展的效率对原始模型的依赖程度很大,因而作者使用neural architecture search来编写了一些列baseline network, 命名为efficient net
Notably, the effectiveness of model scaling heavily depends on the baseline network; to go even further, we use neural architecture search (Zoph & Le, 2017; Tan et al., 2019) to develop a new baseline network, and scale it up to obtain a family of models, called EfficientNets.
Related Work
ConvNet Accuracy
目前以增大模型参数规模的方式提升accuracy已经进入瓶颈。
Notably, the effectiveness of model scaling heavily depends on the baseline network; to go even further, we use neural architecture search (Zoph & Le, 2017; Tan et al., 2019) to develop a new baseline network, and scale it up to obtain a family of models, called EfficientNets.
ConvNet Efficiency
关于卷积神经网络有许多方法可以进行accuracy和effficiency的tradeoff,因为目前的模型一般都过参数化,导致训练effficeincy很低而对accuracy的提升也很低。
但是减少参数的方法是不易找到的。
However, it is unclear how to apply these techniques for larger models that have much larger design space and much more expensive tuning cost. In this paper, we aim to study model efficiency for super large ConvNets that surpass state-of-the-art accuracy. To achieve this goal, we resort to model scaling.
Model Scaling
对于一个模型采取适应不同计算规模的scale有许多方法,比如对于ResNet就可以进行ResNet18到ResNet200之间的伸缩。本文作者将系统化的研究和总结model scaling的方法,关于depth,width,resolution
Compound Model Scaling
Problem Formulation
本小节中作者使用符号语言定义了Model Scaling问题。
我们显然可以认为网络中第i层(Layer i)可以视作一个函数\(Y_i(X) = F_i(X)\),其中\(F_i,X_i,Y_i\)分别为operater,输入输出tensor,具有\(<H_i,W_i,C_i>\)的形状。
那么我们可以认为整个网络可以表达为 \[ N = F_k \bigodot F_{k-1}...\bigodot F_1 (X) = \bigodot _{j=1,2,..k} F_j(X) \] 由于往往神经网络中往往每个layer会分成多个具有相同结构的stage,因此网络也可以表达为 \[ N = \bigodot _{i=1...s} F_i ^{L_i} (X_{<H_i,W_i,C_i>}) \] 其中\(s\)为网络layer的数量,\(L_i\)表示Layer i中的stage数量,\(X_{<H_i,W_i,C_i>}\)表示每一个layer的原始输入,\(F_i\)表示每一个layer中同构stage的operator。
为了限定优化的空间,我们规定scale modeling只能通过在depth,width,resolution上乘系数。 \[ \max _{d,w,r} Accuracy(N(d,w,r)) \\ s.t. \ N(d,w,r) = \bigodot _ {i=1...s} \hat{F} ^{d\cdot \hat{L}_i} (X_{<r\cdot \hat{H}_i,r\cdot \hat {W_i},w \cdot \hat{C_i}>}) \\ Memory(N) \le target\_momory \\ FLOPS(N) \le target\_flops \] 于是优化问题就简化到上述形式,其中\(d,w,r\)分别是depth,width,resolution的scaling系数。
而\(\hat{F_i},\hat{L_i},\hat{H_i},\hat{W_i},\hat{C_i}\) 是baseline network中预定义的参数。
Scaling Dimensions
Depth
传统卷积神经网络调整规模最常用的方法就是改变网络的深度,然而即便是有Skip Connection,Batch Normalization 这样的技巧,更深的网络仍然存在梯度消失问题。
并且网络accuracy能力的提升不仅使得训练的efficiency下降,并且深度增加的边际收益不断缩小。
事实上ResNet101的性能和ResNet1000具有接近的accuracy。
owever, deeper networks are also more difficult to train due to the vanishing gradient problem (Zagoruyko & Komodakis, 2016). Although several techniques, such as skip connections (He et al., 2016) and batch normalization (Ioffe & Szegedy, 2015), alleviate the training problem, the accuracy gain of very deep network diminishes: for example, ResNet-1000 has similar accuracy as ResNet-101 even though it has much more layers. Figure3 (middle) shows our empirical study on scaling a baseline model with different depth coefficient d, further suggesting the diminishing accuracy return for very deep ConvNets.
Width
增加width(通道数)理论上会增加网络捕捉输入形状的能力, 然而经验表明浅而极度宽的网络并不能捕获高阶的形状信息,并且accuracy收益同样是随着width增加而递减的。
Resolution
增加分辨率确实能够提升accuracy, 约复杂的任务往往使用更高的分辨率。而同样的resolution提高的同时,accuracy提升收益也在递减。
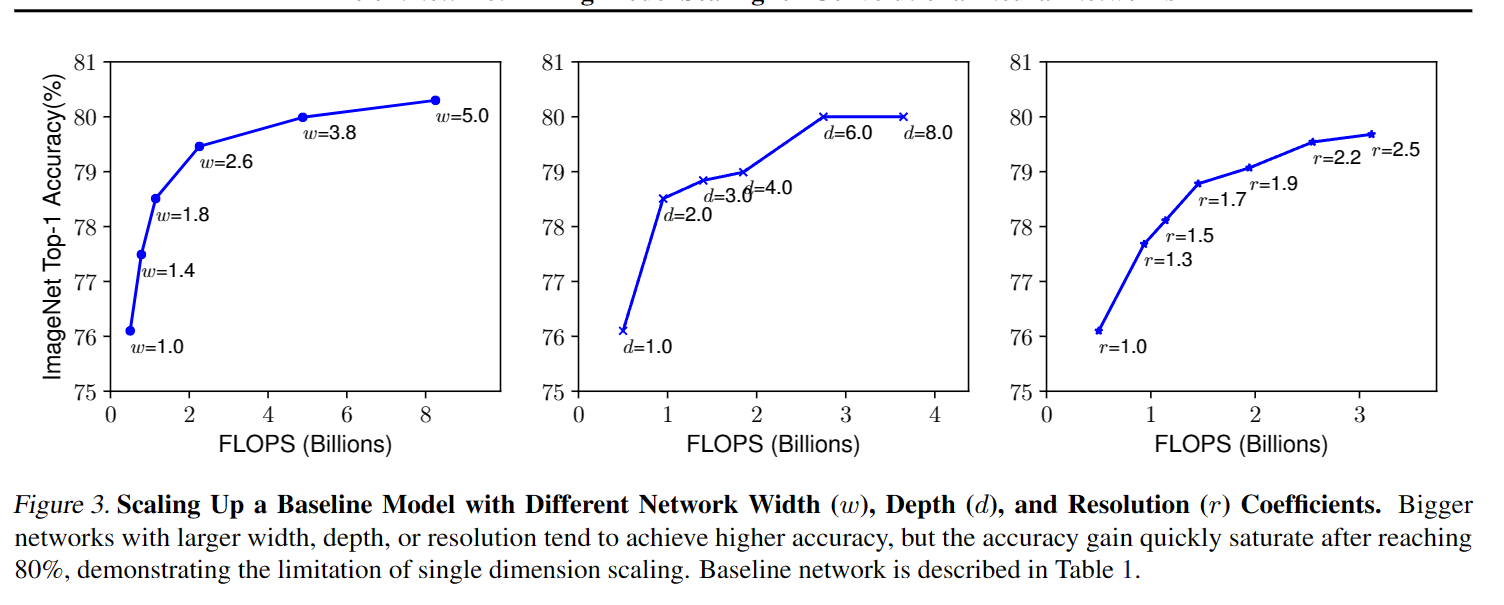
所以作者在这里得到第一条观察结论,提升任一网络参数(d,w,r)的边际收益都是递减的。
Observation 1 – Scaling up any dimension of network width, depth, or resolution improves accuracy, but the accuracy gain diminishes for bigger models.
Compound Scaling
上一节中表面在Model Scaling中我们应该在不同维度中做协调和平衡,而非对单一维度做scale。
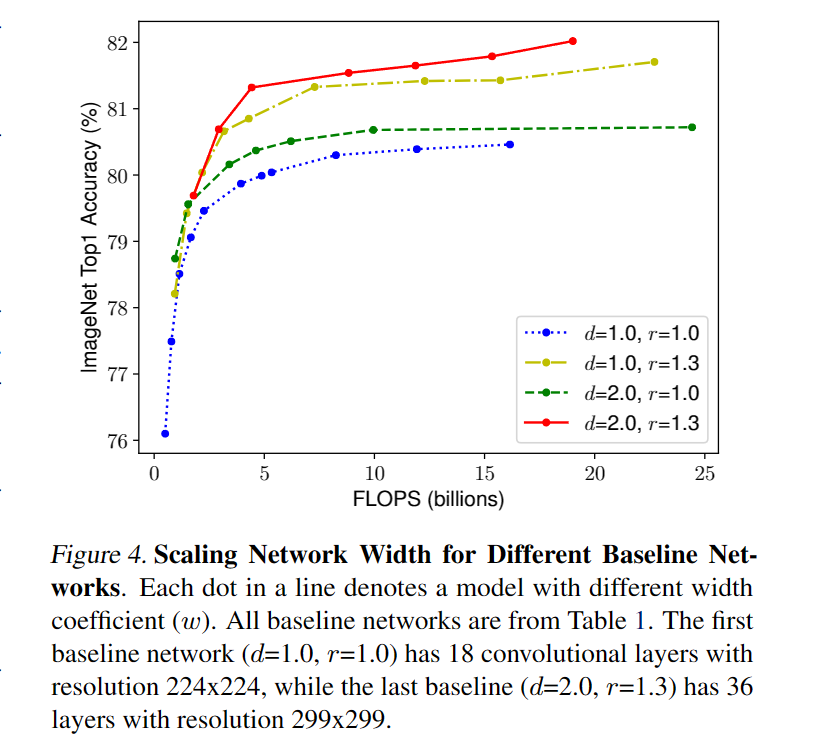
作者根据上图中的实验结果得到第二条观察结论:为了追求网络的accuracy和efficiency,平衡网络的深度,宽度和分辨率在scaling过程中是至关重要的。
事实上已经有一些以前的工作尝试任意改变网络的三维(深度宽度分辨率),但是需要大量的手工调节工作。
本文作者则提供了一种新的compound scaling method \[ depth:d=\alpha^{φ} \\ width:w=\beta^{φ} \\ resolution: r=\gamma ^{φ} \\ s.t. \ \alpha \cdot \beta ^{2} \cdot \gamma ^2 \approx 2 \\ \alpha \ge 1,\beta \ge 1,\gamma \ge 1 \] 在这里值得注意的是常规的卷积网络的FLOPS与\(d,w^2,r^2\)成正比。
因而根据上式,FLOPS应当与\((\alpha \cdot \beta ^2 \cdot \gamma ^2)^{φ}\)成正比。
这样设计的目的是为了方便估计FLOPS的增长情况。