深度学习入门笔记1
本文记录了本人阅读《深度学习入门:基于Python的理论与实现》(斋藤康毅)一书做的一些笔记。
1 感知机
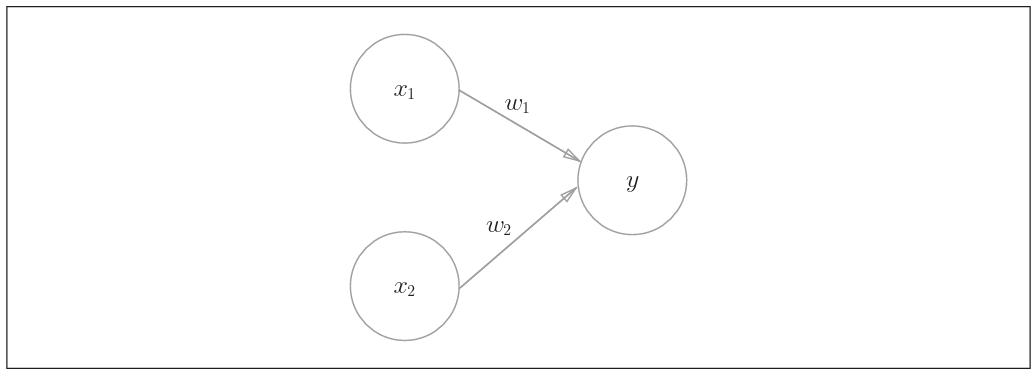
感知机接收多个输入信号,输出一个信号。这里所说的“信号”可以想 象成电流或河流那样具备“流动性”的东西。像电流流过导线,向前方输送 电子一样,感知机的信号也会形成流,向前方输送信息。但是,和实际的电 流不同的是,感知机的信号只有“流/不 流 ”( 1/0)两种取值。在《深度学习入门:基于Python的理论与实现》中,0 对应“不传递信号”,1对应“传递信号”。
而$w_1,w_2$是信号的权重,感知机的工作模式可以用以下公式描述。
此处的$\theta$应理解为一个阈值。
上式也可写作
其中$b$称为偏差, 反应感知机易于激活的程度。
也可以将感知机中的偏差$b$显示地表达出来
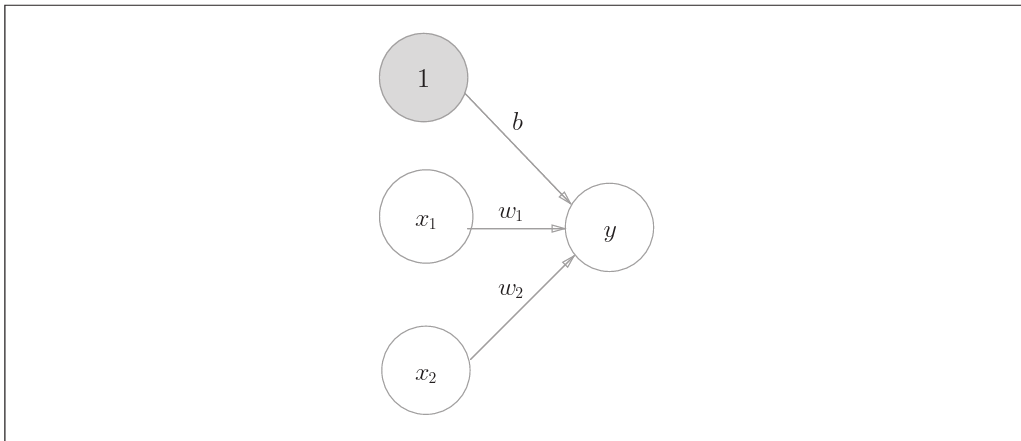
将上式进一步简化后可表达为
2 神经网络
2.1 神经网络层
一个神经网络的例子,本书中将输入层,中间层,输出层依次作为0,1,2层
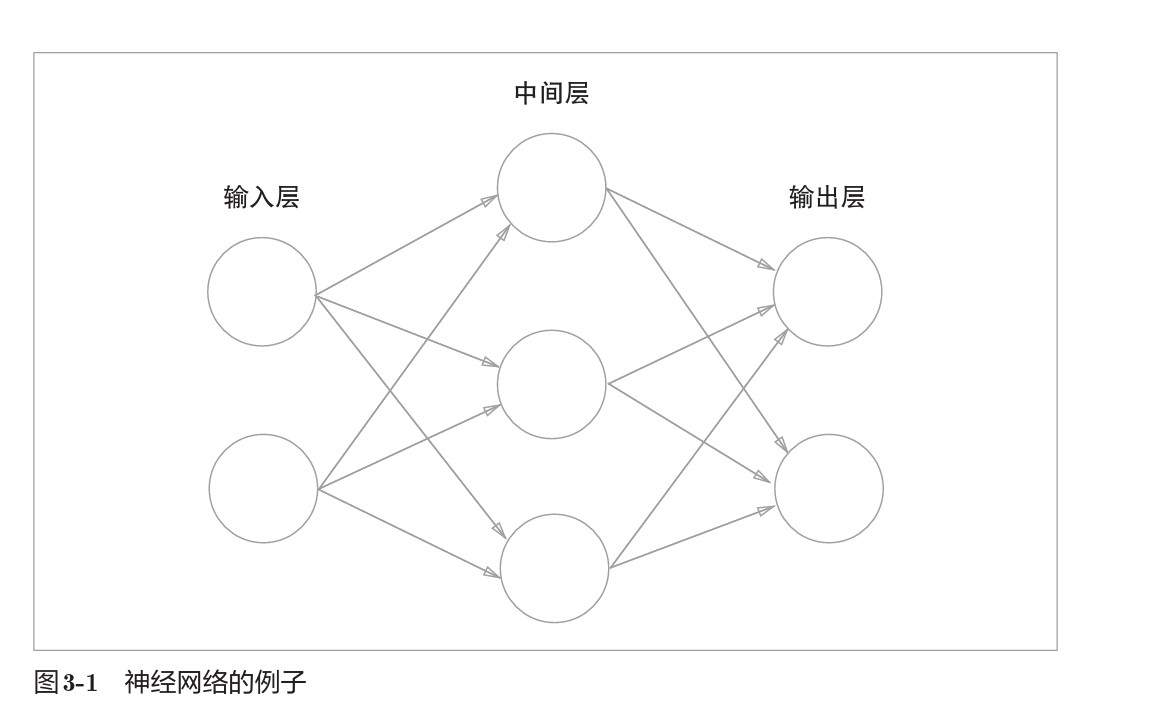
2.2 激活函数
在感知机部分中我们引入过$h(x)$, 这类函数一般都是将输入信号总和转为一个输出信号。
在感知机中的工作模式如下
在感知机中显示得表达出$h(x)$的工作
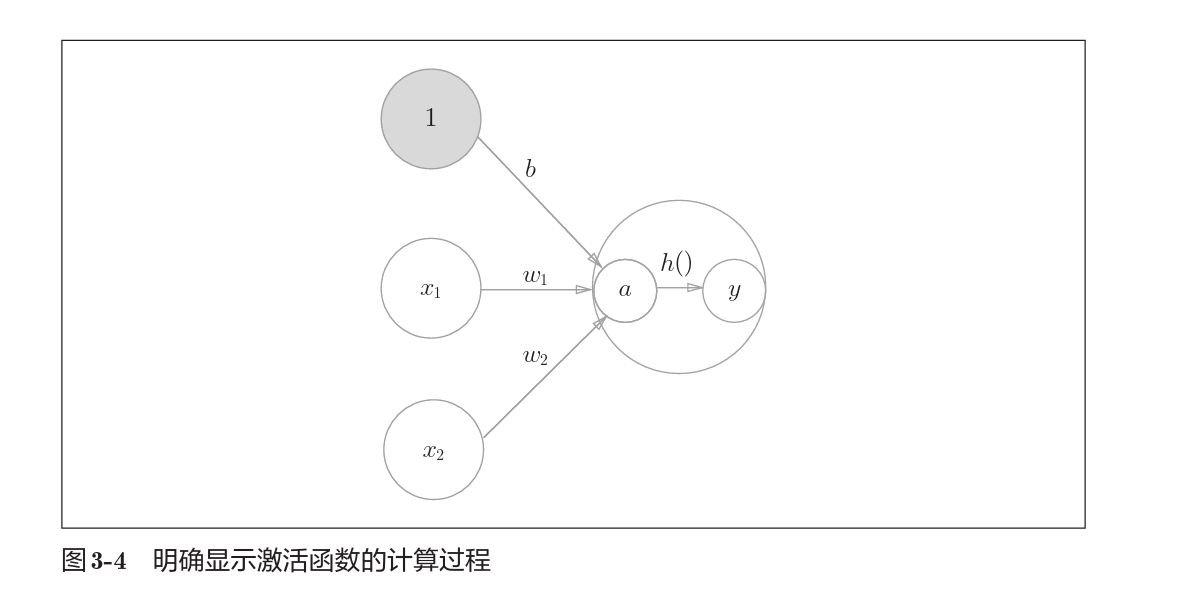
2.2.1 sigmod函数
sigmod函数是一种常见的激活函数。
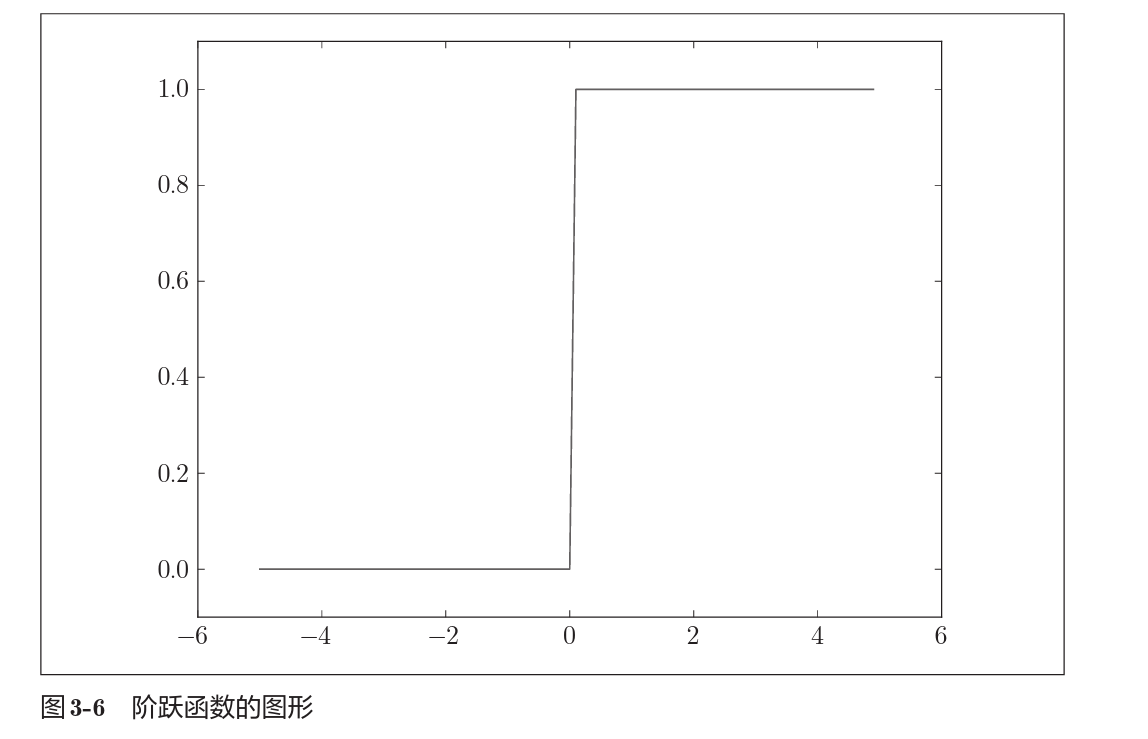
2.2.2 阶跃函数
阶跃函数很简单,就是根据一个阈值将连续输入转为离散化的输出,和第一部分感知机中讲述的$h(x)$ 是一样的,类似于我们在学微积分时候的sign函数。
以下是阶跃函数和sigmod函数的图像对比。
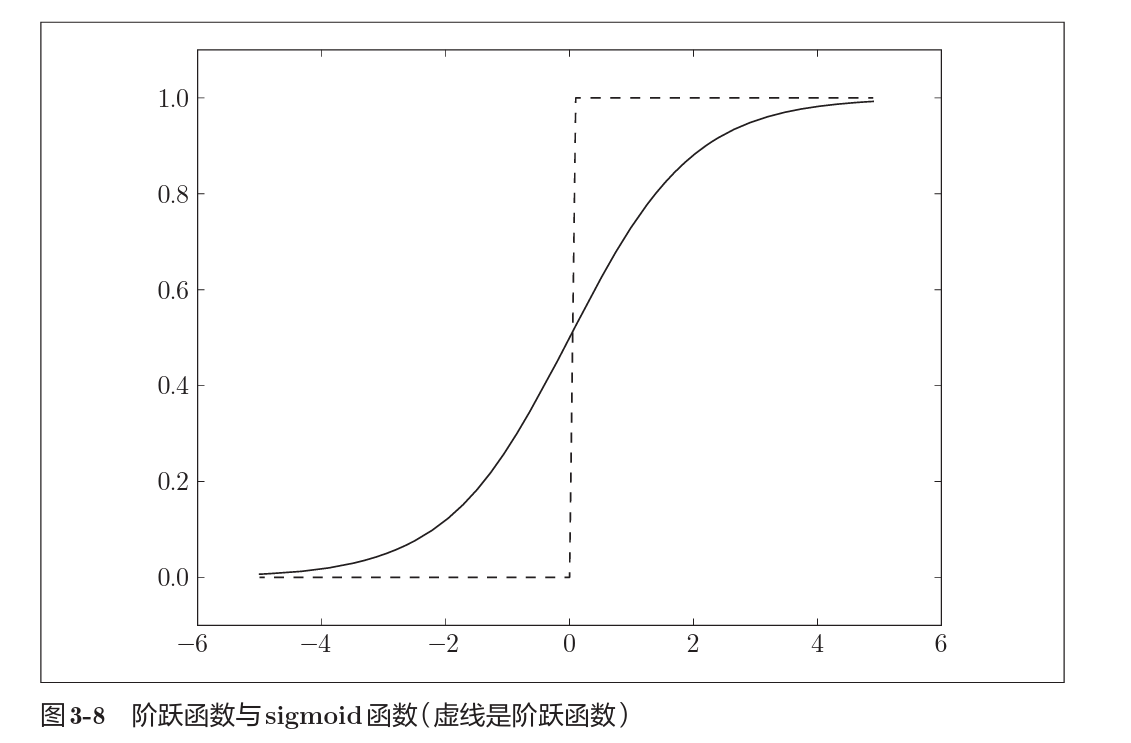
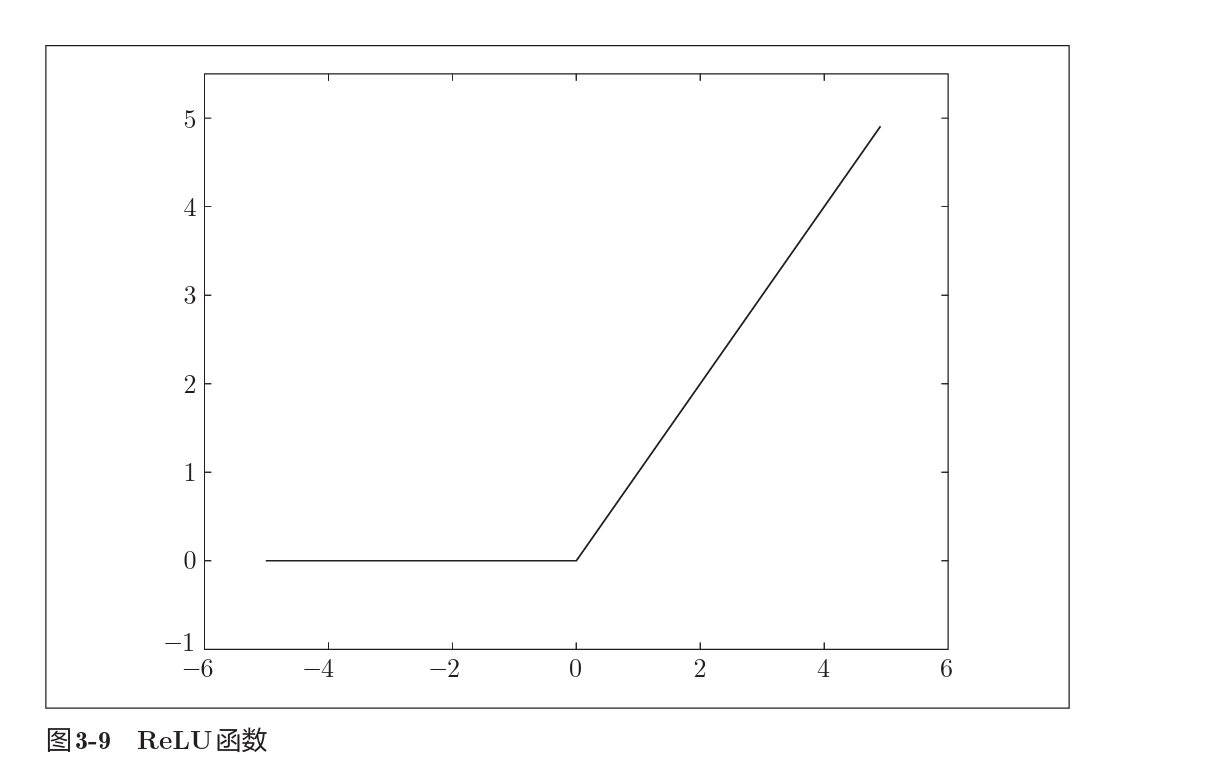
2.2.3 ReLU
ReLU函数是近来使用较多的函数。
2.3 神经网络的内积
神经网络的运算基础是通过矩阵的乘法,示意图如下
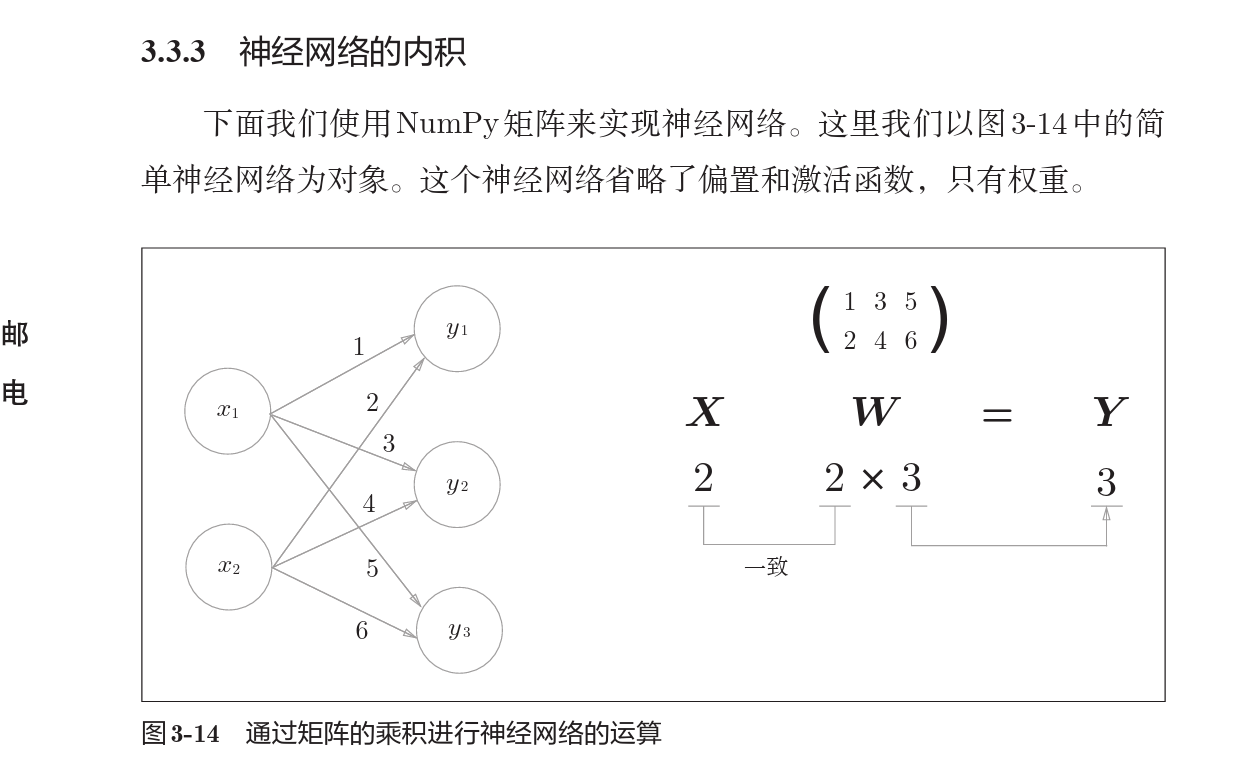
多层神经网络如下图
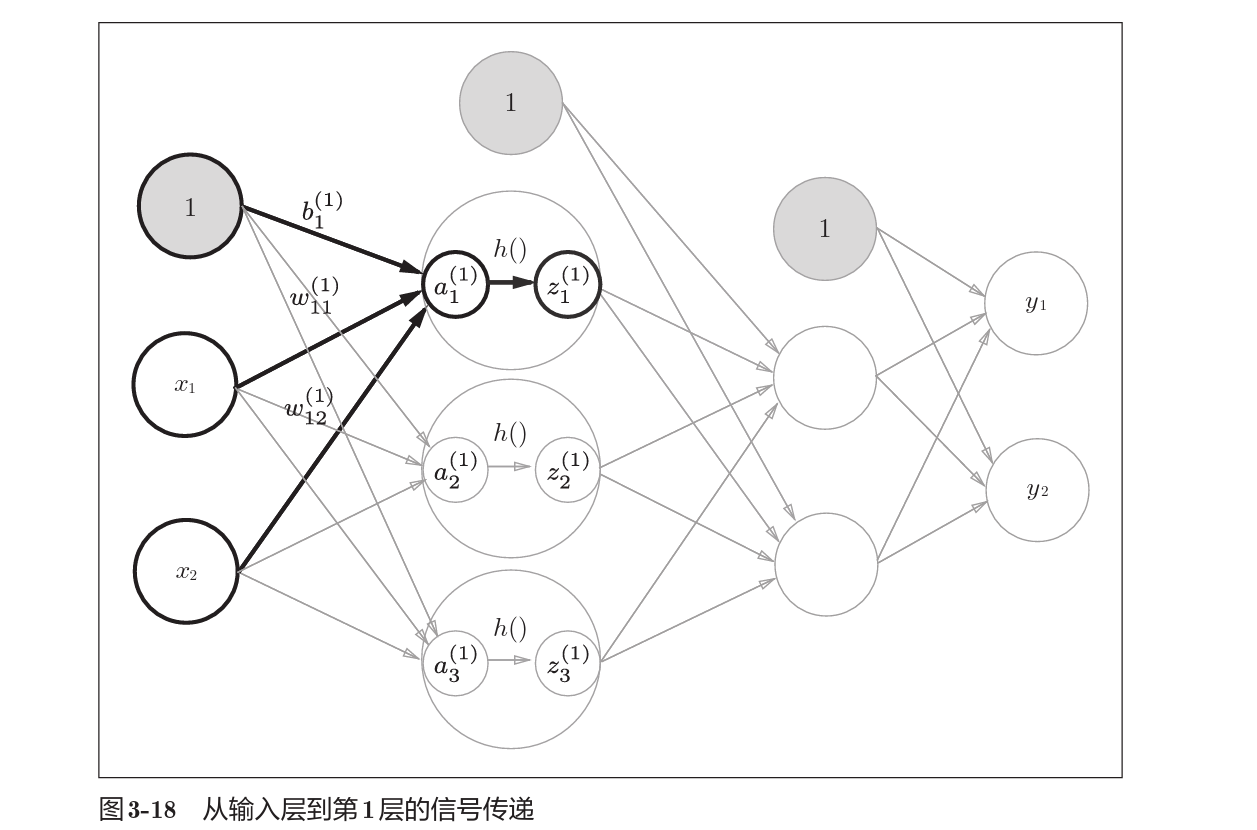
3 神经网络的学习
前面介绍了神经网络的工作模式,不难看出,保证神经网络正确工作(完成识别,分类等任务)的关键在于权重和神经元的数量。
神经网络的关键点就在于如何从数据中学习,获得正确的参数。
训练数据和测试数据
机器学习中,一般将数据分为训练数据和测试数据两部分来进行学习和 实验等。首先,使用训练数据进行学习,寻找最优的参数;然后,使用测试 数据评价训练得到的模型的实际能力。
为什么需要将数据分为训练数据和测 试数据呢?因为我们追求的是模型的泛化能力。为了正确评价模型的泛化能 力,就必须划分训练数据和测试数据。另外,训练数据也可以称为监督数据。
仅仅用一个数据集去学习和评价参数,是无法进行正确评价的。 这样会导致可以顺利地处理某个数据集,但无法处理其他数据集的情况。顺 便说一下,只对某个数据集过度拟合的状态称为过拟合(over fitting)。
损失函数
损失函数(loss function)描述的是神经网络性能的恶劣程度,一般使用均方误差和交叉熵。
均方误差
其中,$y_k,t_k$分别表示神经网络的输出,监督数据,神经网络的输出和监督数据的差异的均方体现为均方误差。
交叉熵误差
采用交叉熵策略的道理是一般监督数据$t_k$往往采用独热码(one hot),因此在正确标签的位是1,其余为0。
因此交叉熵误差事实上是测试的是在监督数据输出为正确的情况下,神经网络输出的误差。
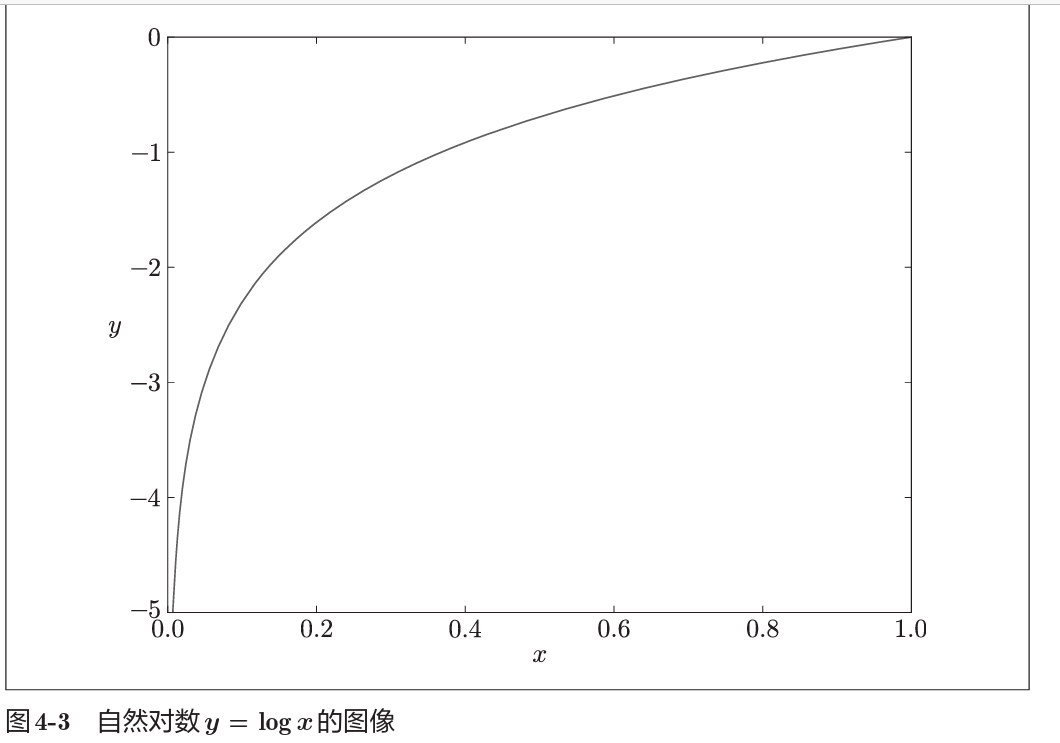
根据自然对数图像,很自然地,神经网络输出值越接近1(即正确值),交叉熵误差就越小。
mini-batch
使用mini-batch的理由很自然,神经网络的训练数据集往往规模巨大,如果以全部数据为对象计算损失函数是成本巨大的。
因此我们往往从数据集中选出一部分来作为全部数据的近似,称为mini-batch,即小批量。
梯度法
关于函数,导数,偏导数,数值微分,梯度的概念自行查阅微积分资料。
机器学习的主要任务就是在学习时寻找最优参数(权重和偏置)
我们可以将神经网络的损失函数$L$看作是关于权重的多元函数.
一般而言,神经网络参数空间巨大,$L$ 往往无法得到解析的表示,而我们只需要得到$L$的极小值点就可以达到优化的目的,我们认为$L$ 关于参数空间是连续且可微。
那么我们可以利用数值微分的方法得到$L$关于某参数$w_k$ 的数值微分
进而我们得到L的梯度
利用梯度下降进行优化的迭代步骤如下:
其中$\eta$为学习率,即权重向梯度方向迭代的步长。
总结
总结神经网络的学习算法,步骤如下:
- mini-batch
- 计算梯度
- 更新参数
- 重复步骤1,2,3到阈值
由于使用的数据是随机的mini-batch数据,因此上述方法又称为随机梯度下降法。
误差反向传播法
计算图
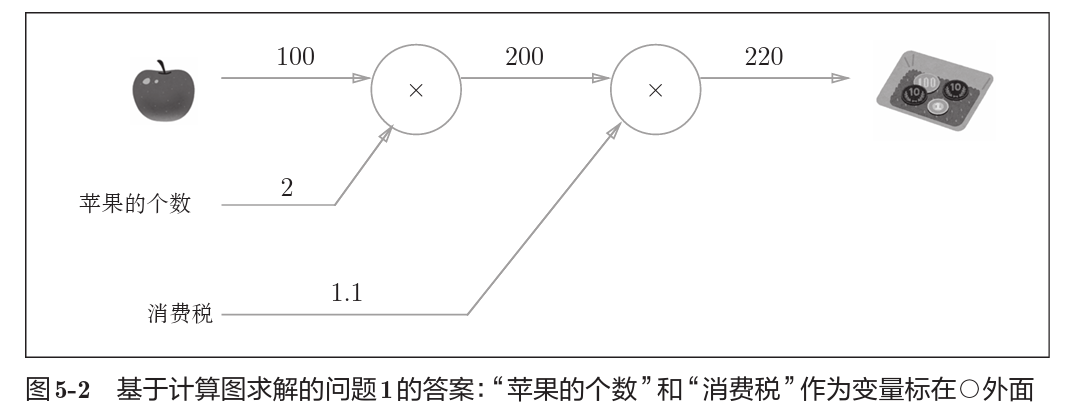
这是一个最简单的计算图,描述的是买苹果的过程中,在苹果数量,单价,消费税三者作用下如何得到最终开销。
使用计算图描述计算过程的好处一是能够进行局部计算,二是能够通过误差反向传播法求导数。
利用误差反向传播求导
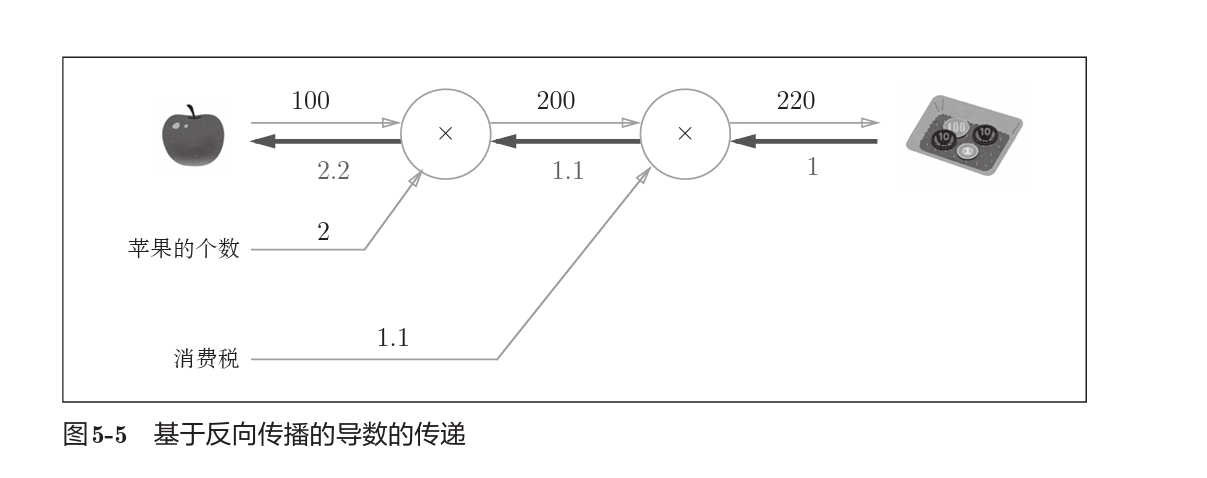
上图是一个用误差反向传播求出导数的例子(苹果的单价,总价对最终价格影响的贡献)。
链式法则
利用计算图进行反向传播计算导数的过程是从右向左传递,与我们日常接触的计算恰恰相反。
传递导数的原理在于链式法则。
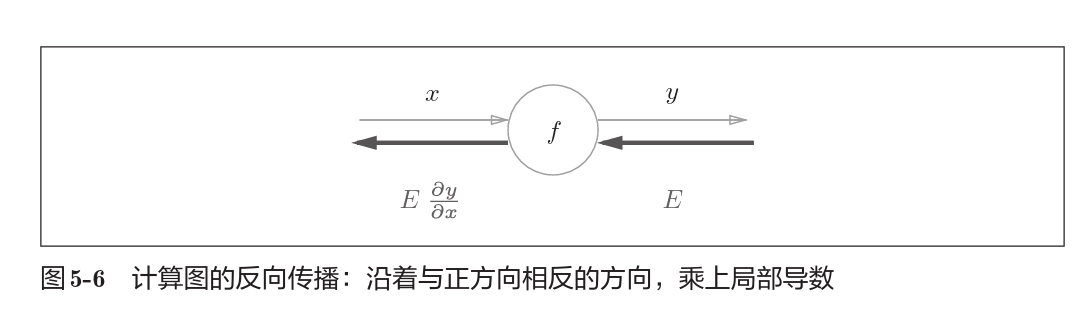
假设存在$y=f(x)$的计算,反向传播如上图所示。
$E$信号是右侧传来的信号,乘以$f$节点的局部导数$\frac{\partial y}{\partial x}$ 后作为新的导数信号向左侧传递。
事实上可以看出反向传播的过程遵循链式法则。
即$z = f(t),t=f(x)$,那么$\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \frac{\partial t}{\partial x} $
链式法则是复合函数求导的性质,具体查阅微积分教材。
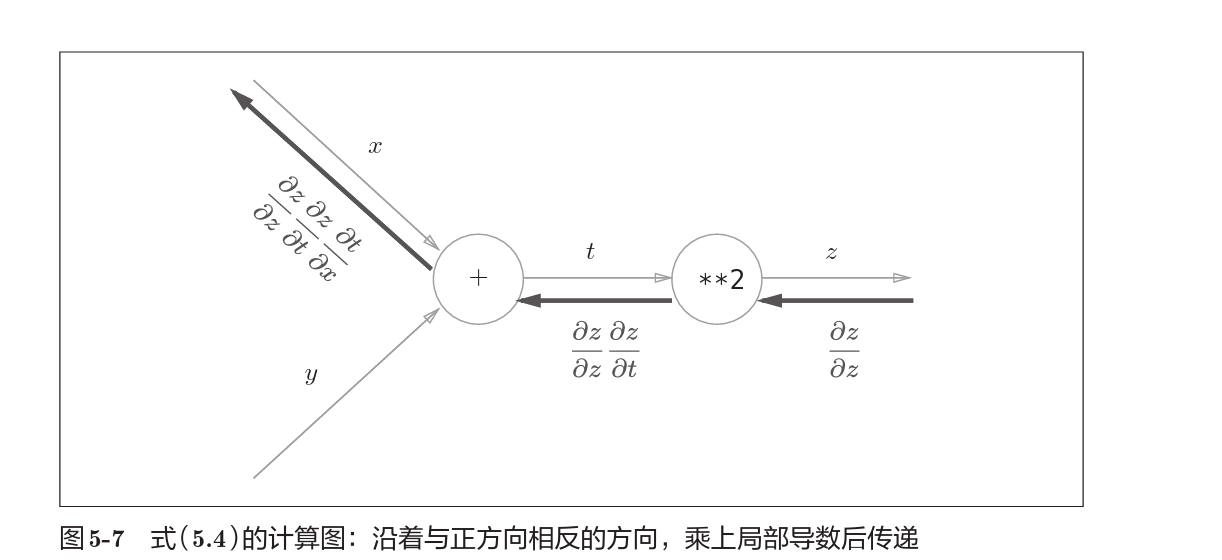
使用链式法则表示的计算图过程如上。
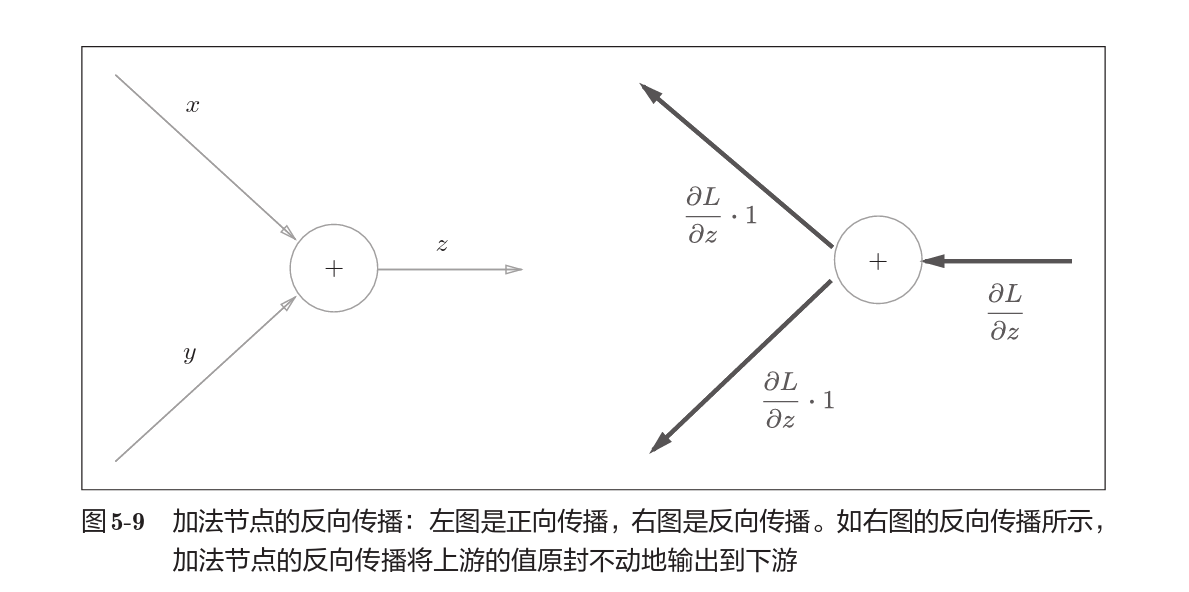
加法节点的反向传播
以$z = x+y$为对象,那么$\frac{\partial z}{\partial x} = \frac{\partial z}{\partial y} = 1$
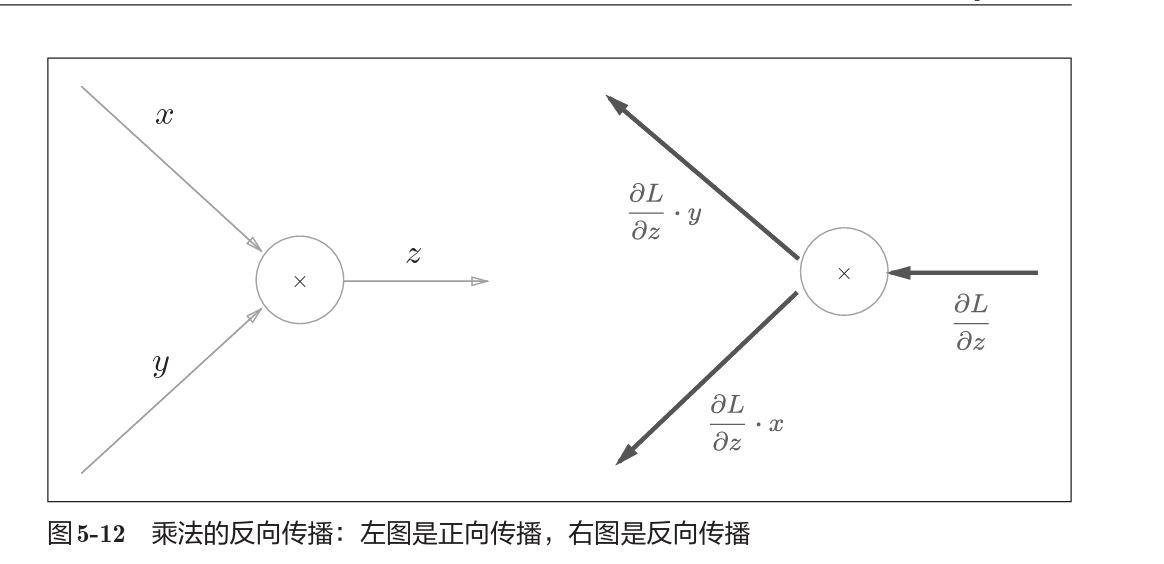
乘法节点的反向传播
以$z = xy$为对象,那么$\frac{\partial z}{\partial x} =y, \frac{\partial z}{\partial y} = x$
实例代码
有反向传播机制的加法层和乘法层。
1 | class AddLayer: |
1 | class MulLayer: |
考虑激活层的情形
考虑ReLU
那么,
对于sigmoid,
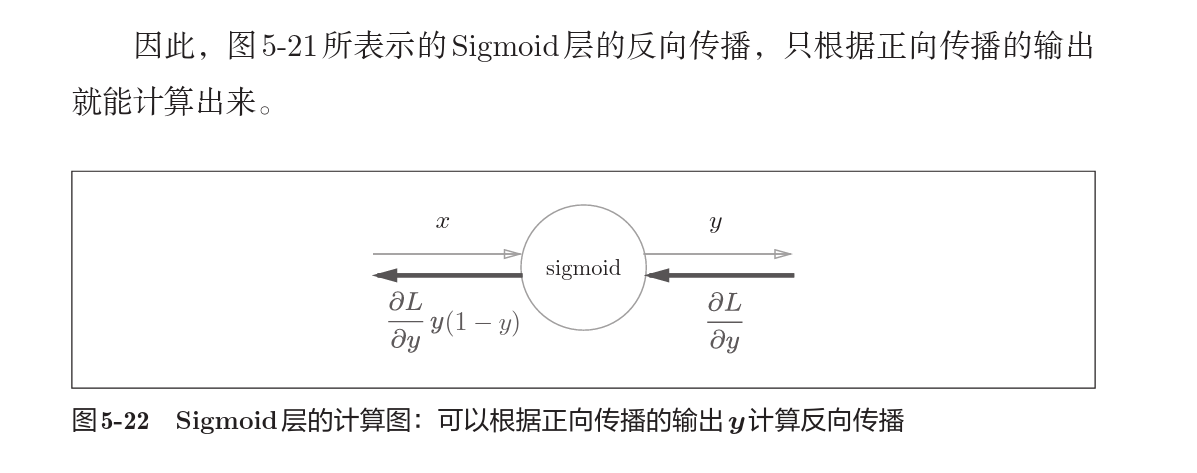
考虑Affine层的实现
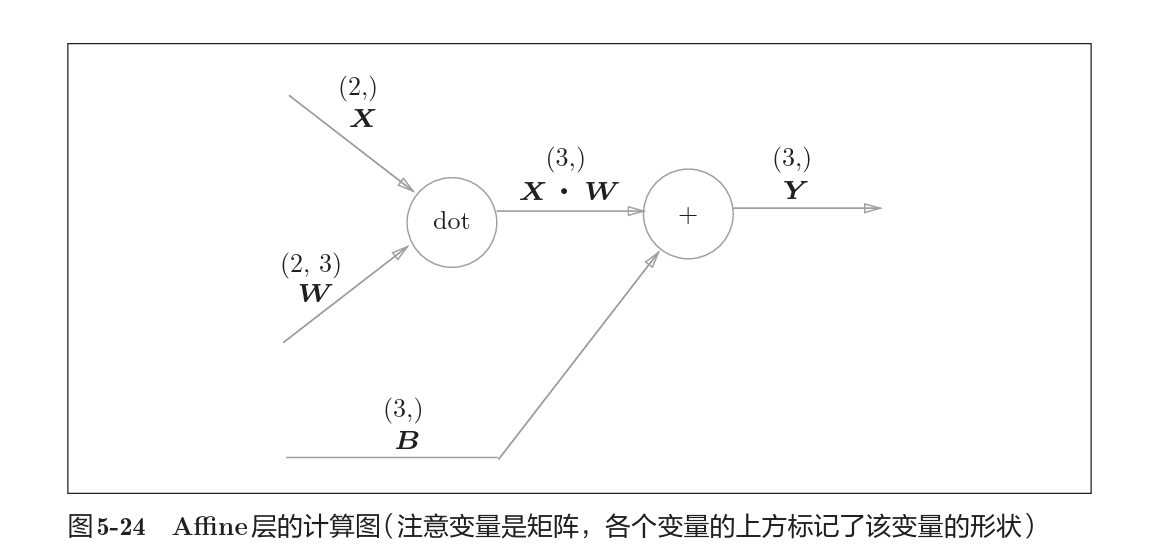
Affine层实际上就是考虑了矩阵运算的清醒,事实上对于矩阵运算的反向传播,有下式
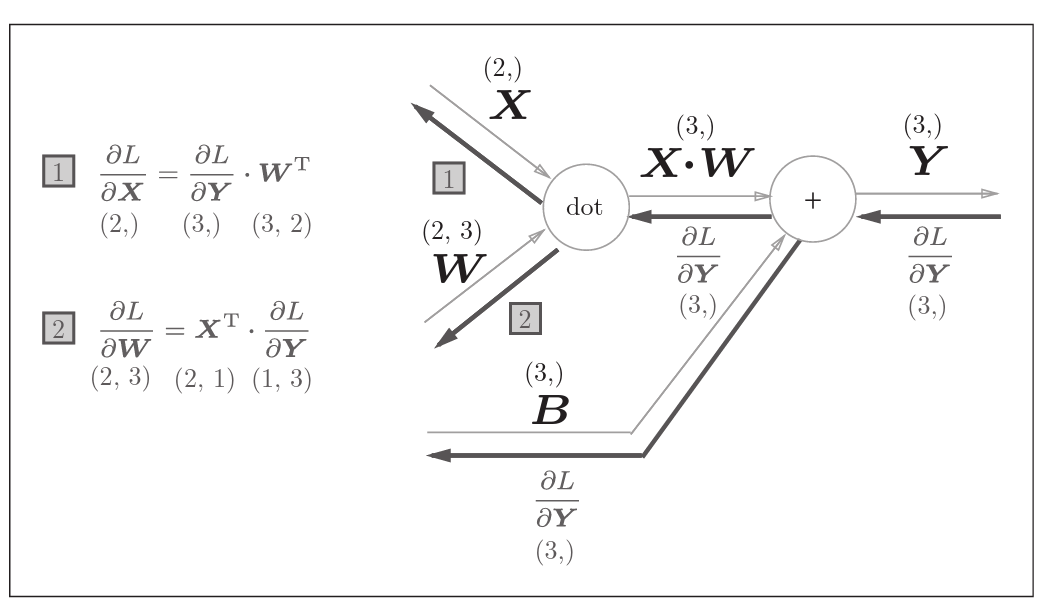
使用误差反向传播法的学习
两层神经网络层的实现
1 | class TwoLayerNet: |
将前文中利用梯度下降求梯度的方法替换为使用误差反向传播。
1 | import sys, os |
卷积神经网络
卷积神经网络即CNN,(Convolutional Neural Network)
常常用于图像识别,语音识别等场合。
整体结构
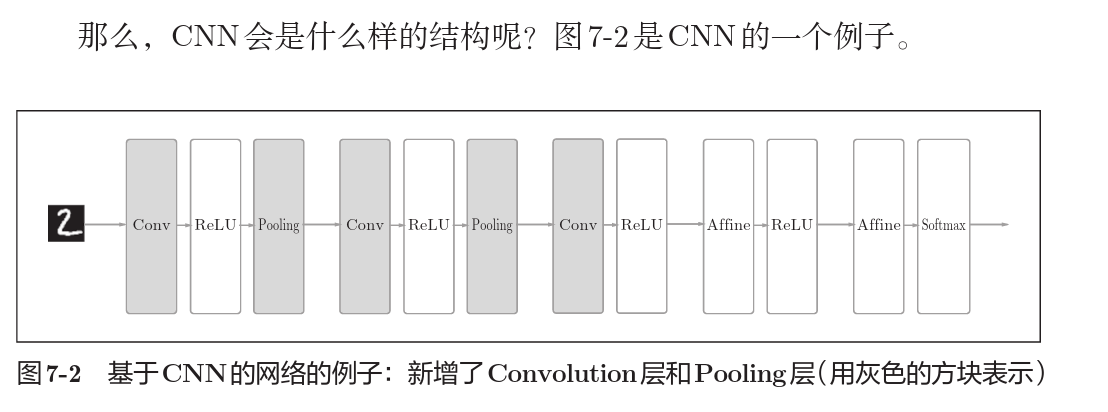
CNN结构和之前的神经网络结构类似,但是出现了卷积层(convolutional)和池化层(pooling)。
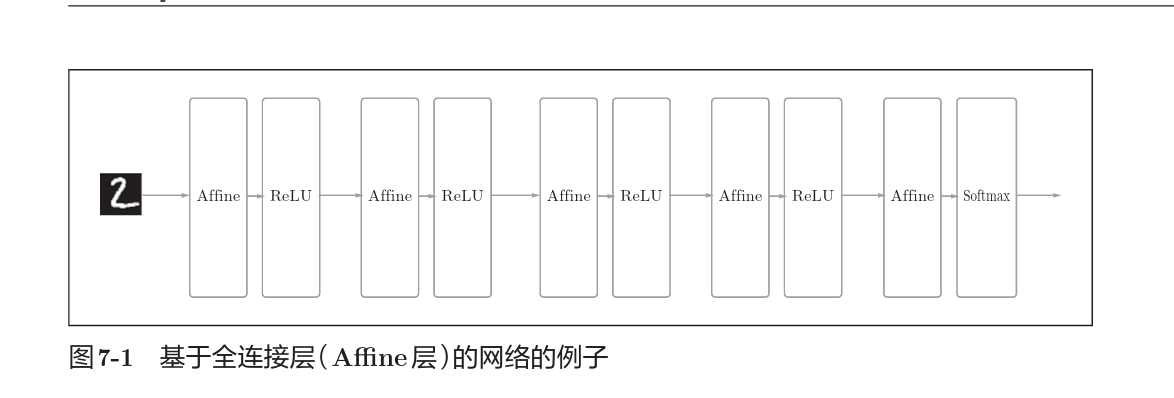
相邻神经元都有连接的结构称为全连接结构,上图在Affine层实现了全连接。
那么在CNN中增加了卷积层和池化层后则如下图所示。
卷积运算
全连接层存在的问题就是全连接层输入时将多维数据拉成一维数据,损失了输入的形状信息,而卷积层则是在保留输入形状信息的基础上进行运算的。
而卷积层可以保持形状不变。当输入数据是图像时,卷积层会以3维 数据的形式接收输入数据,并同样以3维数据的形式输出至下一层。因此, 在CNN中,可以(有可能)正确理解图像等具有形状的数据。
另外,CNN中,有时将卷积层的输入输出数据称为特征图(feature map)。其中,卷积层的输入数据称为输入特征图(input feature map), 输 出 数据称为输出特征图(output feature map)。本书中将“输入输出数据”和“特 征图”作为含义相同的词使用。
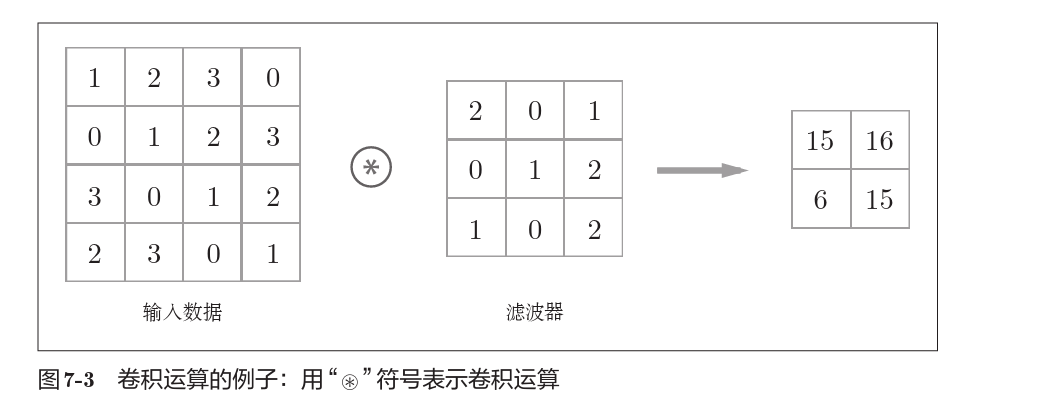
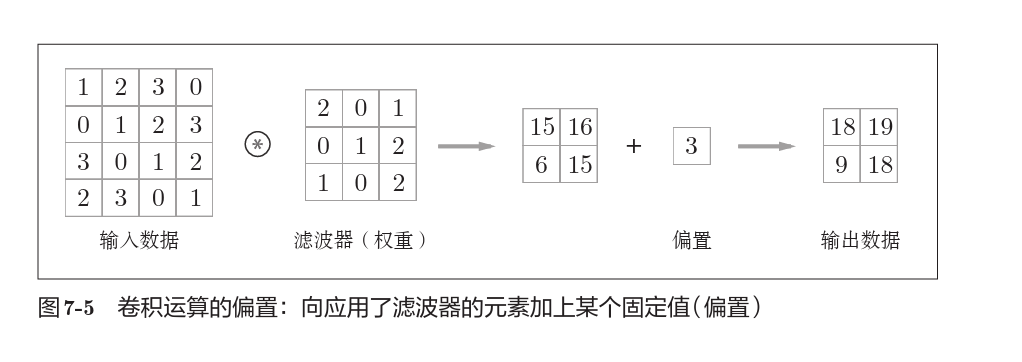
上图是一个卷积运算的例子。
卷积运算事实上是滤波器(也称卷积核)与输入数据各个位置上对应元素相乘再相加。
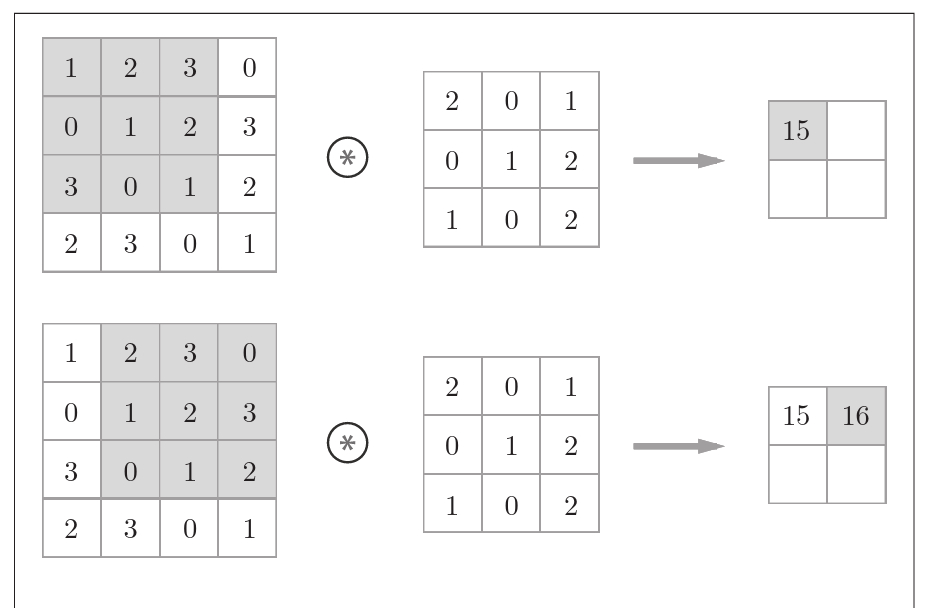
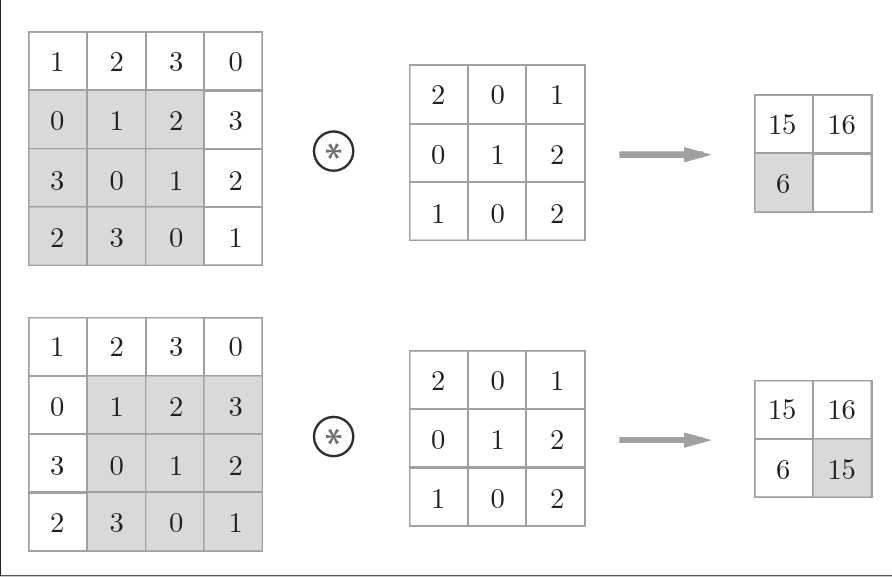
对于偏置,对所有元素进行偏置。
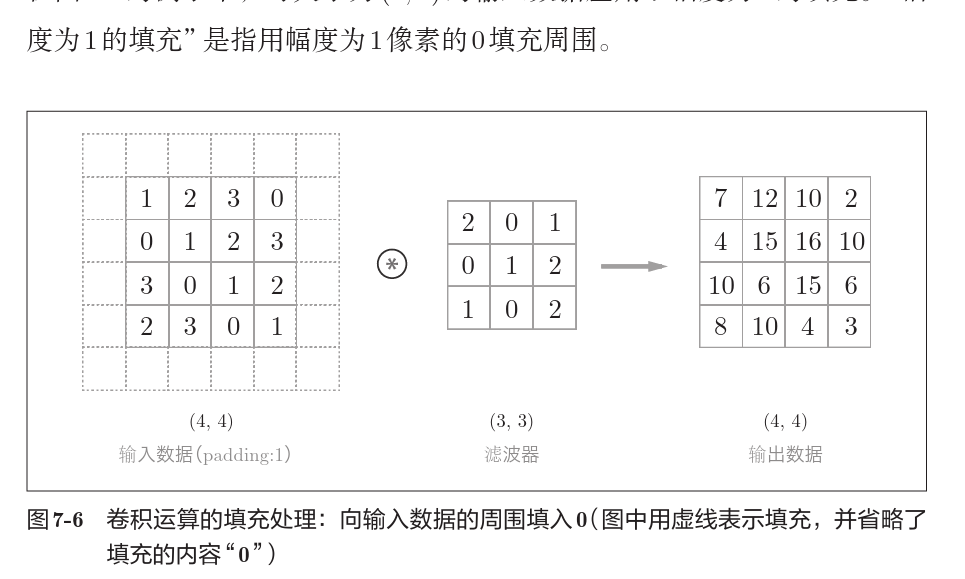
填充
为了控制卷积生成的形状,我们常常要对输入数据先进行填充。
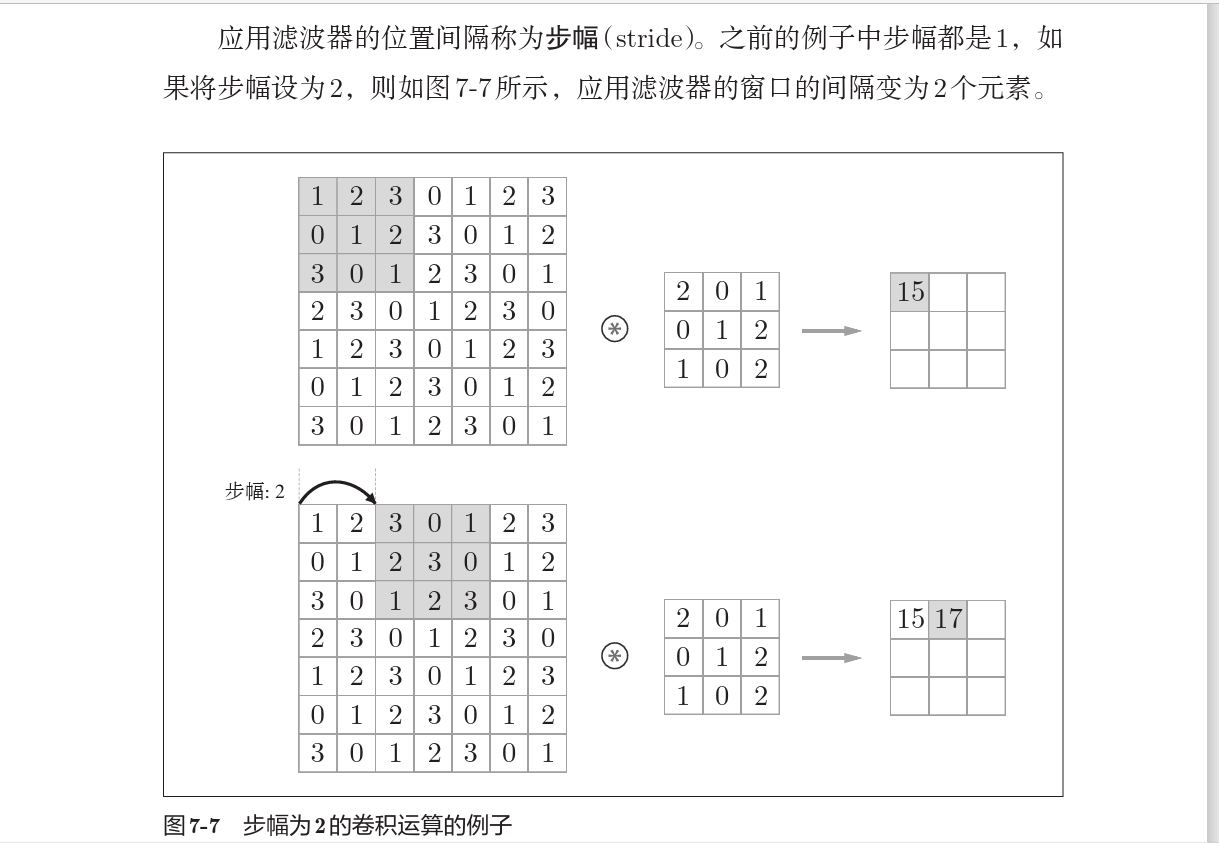
步幅
卷积核在输入数据上移动的步长称为步幅,步幅越大,卷积输出的规模越小。
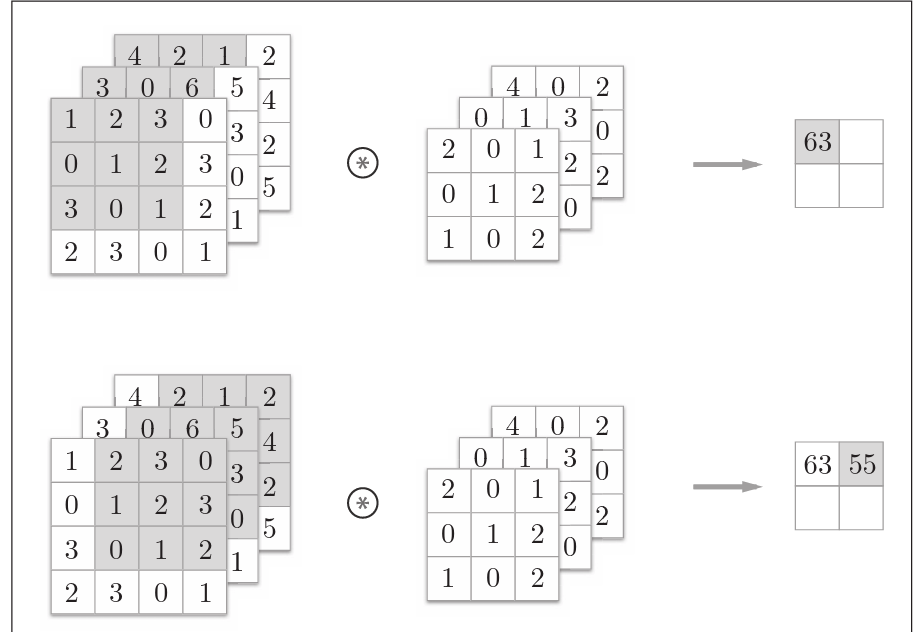
多维数据的卷积运算
这里以3通道的数据为例, 展示了卷积运算的结果。和2维数据时相比,可以发现纵深 方向(通道方向)上特征图增加了。通道方向上有多个特征图时,会按通道 进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出。
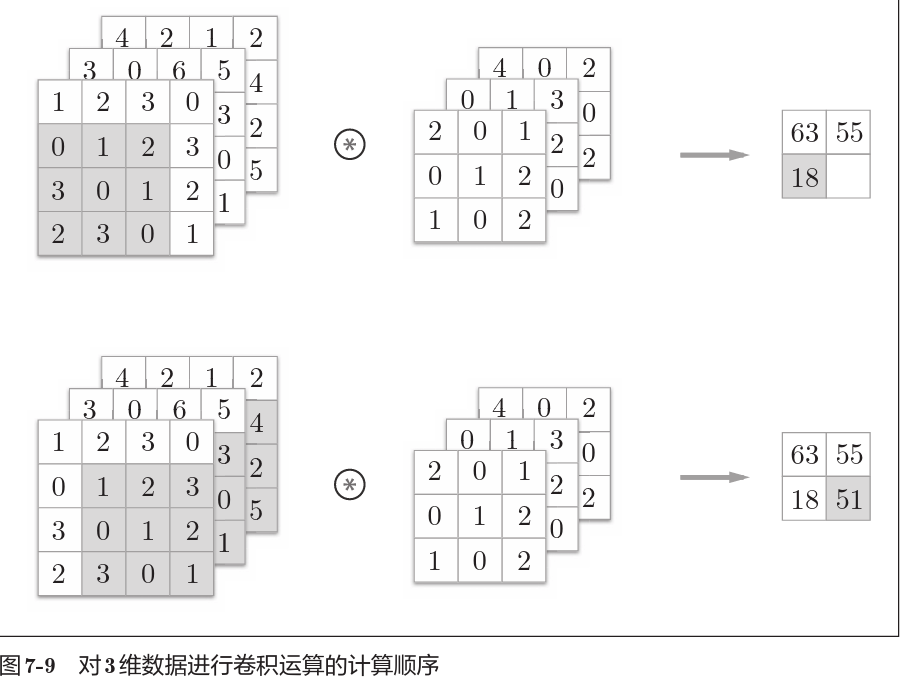
那么如何使得生成结果中具有更多维度呢?
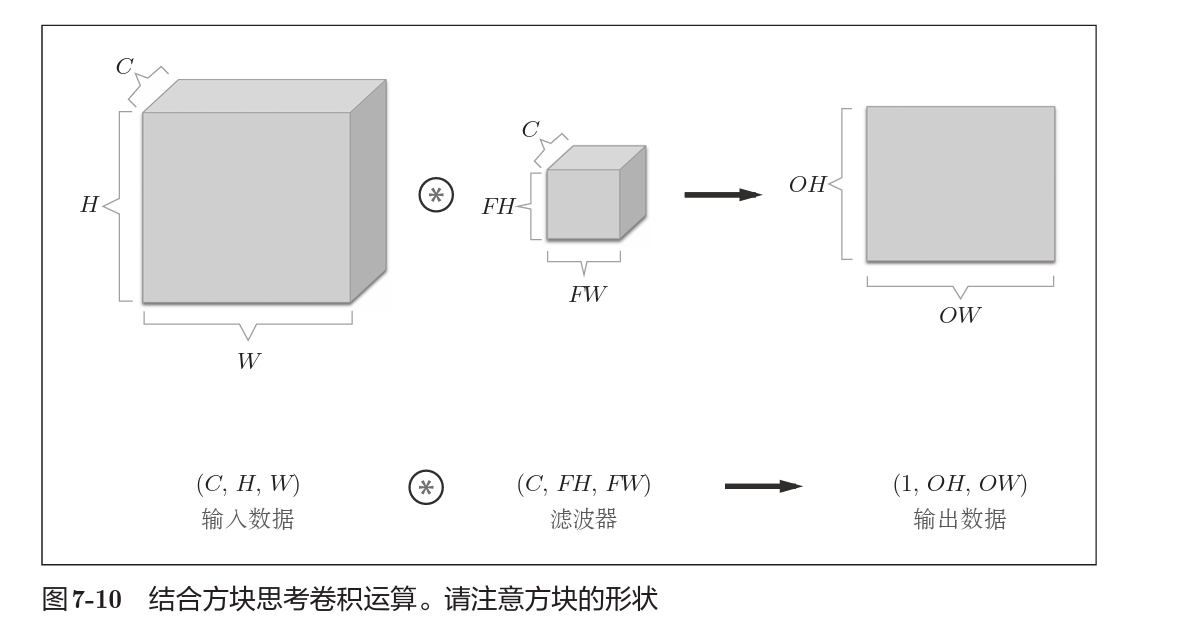
结合方块思考,我们可以将三维矩阵的卷积抽象为上述方块,立方体*立方体得到正方形,
如果想要得到立方体的结果,那么卷积核就要再提高一个维度,也就是将N个卷积核的二维结果拼接成三维。
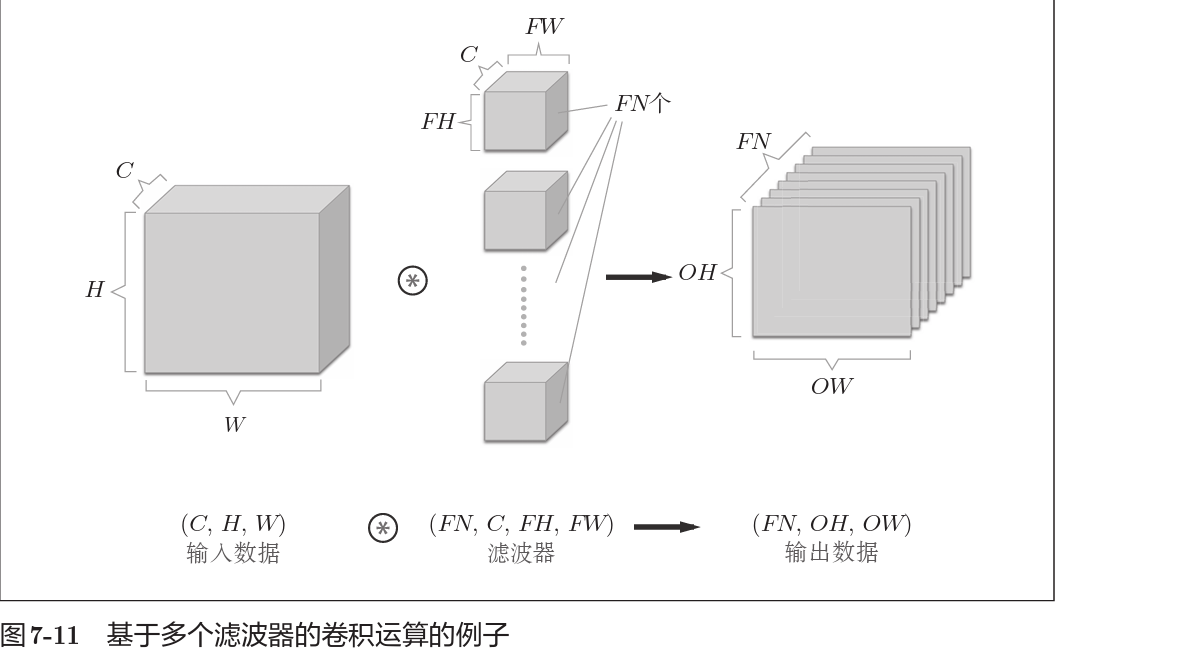
如果应用批处理,那么就在输入数据上再增加一个批维度。
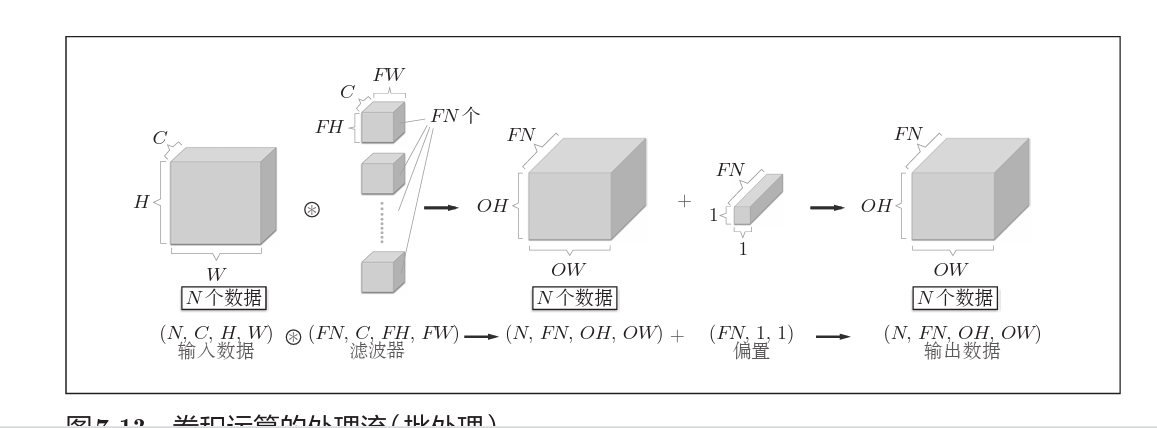
像这样,数据作为4维的形状在各层间传递。这里需要注意的是,网络间传 递的是4维数据,对这N个数据进行了卷积运算。也就是说,批处理将N次 的处理汇总成了1次进行。
池化层
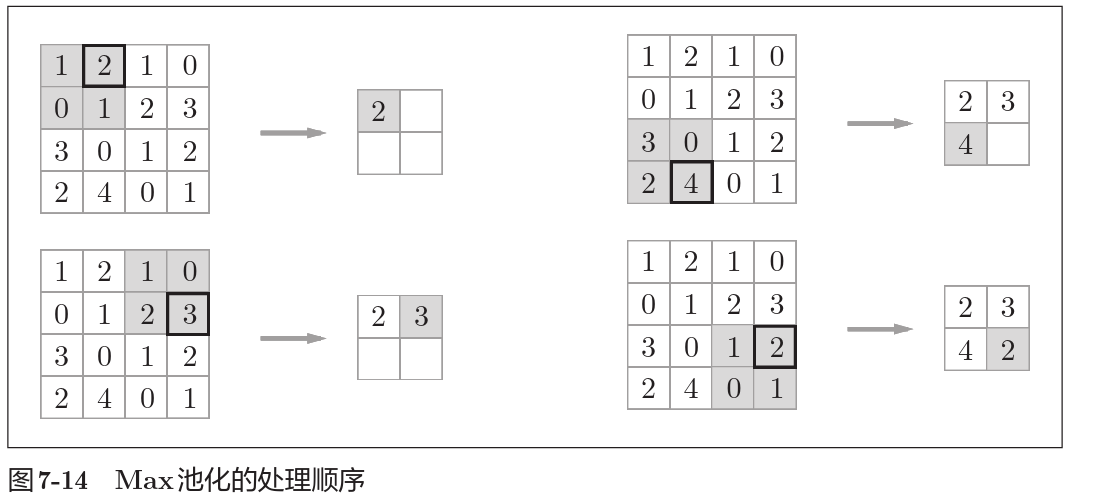
池化运算是缩小矩阵规模的运算,上图中将2*2矩阵缩小为1*1,且应用Max池化,即选取矩阵中最大的元素作为池化结果。
除了Max池化之外,还有Average池化等。相对于Max池化是从 目标区域中取出最大值,Average池化则是计算目标区域的平均值。 在图像识别领域,主要使用Max池化。因此,本书中说到“池化层” 时,指的是Max池化。
池化层具有如下特征:
- 没有要学习的参数
- 通道数不发生改变
- 对微小变化具有鲁班性,可以理解为应用max池化时,块中非max元素的改变对池化结果没有影响。